Equation Of Conic Sections Polar Form
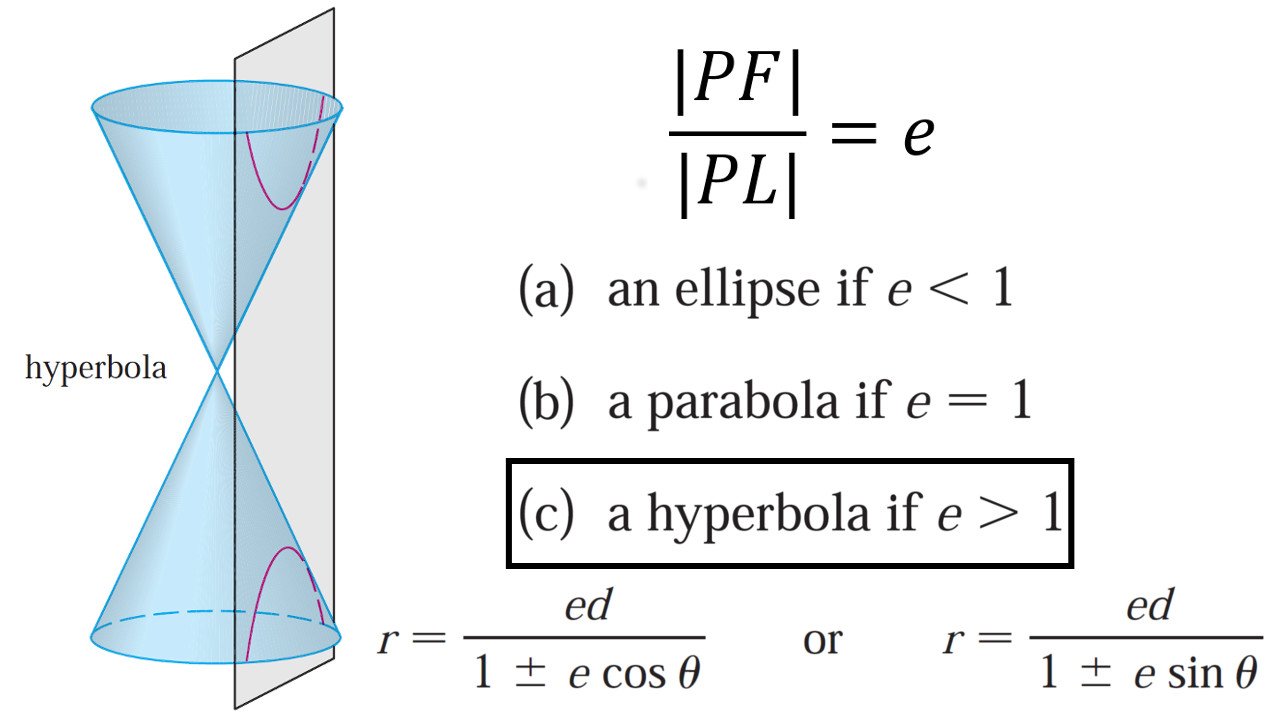
Equation Of Conic Sections Polar Form - For a conic with a focus at the origin, if the directrix is x= ±p, x = ± p, where p p is a positive real number, and the eccentricity is a positive real number e, e, the conic has a polar equation. By the end of this section, you will be able to: Web then the polar equation for a conic takes one of the following two forms: R = when r = , the directrix is horizontal and p units above the pole; Web to work with a conic section written in polar form, first make the constant term in the denominator equal to 1. The coefficients a and c are need to identify the conic sections without having to complete the square.
To convert this cartesian equation to polar form, we will use the substitutions and. Define conics in terms of a focus and a directrix. By the end of this section, you will be able to: Web to work with a conic section written in polar form, first make the constant term in the denominator equal to 1. To identify a conic generated by the equation \(ax^2+bxy+cy^2+dx+ey+f=0\),first calculate.
For a conic with a focus at the origin, if the directrix is x= ±p, x = ± p, where p p is a positive real number, and the eccentricity is a positive real number e, e, the conic has a polar equation. Identify a conic in polar form. Subtract 9 from both sides. Ax2 + bxy + cy2 + dx +ey + f = 0. Define conics in terms of a focus and a directrix.
These definitions are important because they inform how to use conic sections in real. Ax2 + bxy + cy2 + dx +ey + f = 0. Each conic section can be defined as a locus of points. Graph the polar equations of conics. This formula applies to all conic sections.
A and c cannot be 0 when making this determination. I have managed to determine this is an ellipse and write it in a canonical form with changed variables: The coefficients a and c are need to identify the conic sections without having to complete the square. The axis, major axis, or transverse axis of the conic (depending on which.
Polar coordinates allow you to extend your knowledge of conics in a. Multiply the numerator and denominator by the reciprocal of the constant in the denominator to rewrite the equation in standard form. Ax2 + bxy + cy2 + dx +ey + f = 0. To identify a conic generated by the equation \(ax^2+bxy+cy^2+dx+ey+f=0\),first calculate. Web polar equations of conic.
This formula applies to all conic sections. Define conics in terms of a focus and a directrix. Web it explains how to identify the conic as an ellipse, parabola or hyperbola and how to determine the eccentricity and the equation of the directrix of the conic section. For instance, determining the orbits of objects revolving about the sun. For each.
9r2 = + 11 3r cos. R(θ) = ed 1 − e cos(θ − θ0), r ( θ) = e d 1 − e cos. The axis, major axis, or transverse axis of the conic (depending on which type it is) is vertical, on the line θ =. Web x = 2 + y. Multiply the numerator and denominator by.
( θ − θ 0), where the constant θ0 θ 0 depends on the direction of the directrix. Web then the polar equation for a conic takes one of the following two forms: 9.6 conic sections in polar coordinates. Just as two (distinct) points determine a line, five points determine a conic. A locus of points is a set of.
A locus of points is a set of points, each location of which is satisfied by some condition. Subtract 9 from both sides. By the end of this section, you will be able to: Web the polar equation of a conic section with eccentricity e is \(r=\dfrac{ep}{1±ecosθ}\) or \(r=\dfrac{ep}{1±esinθ}\), where p represents the focal parameter. Web for a conic with.
Equation Of Conic Sections Polar Form - Hyperbola → a ⋅ c < 0. R=\frac {ep} {1\pm e\text { }\sin \text { }\theta } r = 1±e sin θep. Web then the polar equation for a conic takes one of the following two forms: By the end of this section, you will be able to: X2 + y2 − xy + x = 4. Ellipse → a⋅ c > 0 and a ≠ c. Parabola → a⋅ c = 0. Web conic sections in polar coordinates. Planets orbiting the sun follow elliptical paths. If we place the focus at the origin, we get a very simple equation of a conic section.
To create a general equation for a conic section using the definition above, we will use polar coordinates. Web for a conic with a focus at the origin, if the directrix is y=\pm p y = ±p, where p p is a positive real number, and the eccentricity is a positive real number e e, the conic has a polar equation. 9r2 = + 11 3r cos. Web given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity. Graph the polar equations of conics.
Web polar equations of conic sections: 9.6 conic sections in polar coordinates. To convert this cartesian equation to polar form, we will use the substitutions and. Web the polar equation for a conic.
Web could someone show me how to find a polar form of this general equation of a conic section? A and c cannot be 0 when making this determination. A locus of points is a set of points, each location of which is satisfied by some condition.
Ellipse → a⋅ c > 0 and a ≠ c. The coefficients a and c are need to identify the conic sections without having to complete the square. Web then the polar equation for a conic takes one of the following two forms:
Ellipse → A⋅ C > 0 And A ≠ C.
R=\frac {ep} {1\pm e\text { }\sin \text { }\theta } r = 1±e sin θep. Parabola → a⋅ c = 0. Define conics in terms of a focus and a directrix. I have managed to determine this is an ellipse and write it in a canonical form with changed variables:
To Create A General Equation For A Conic Section Using The Definition Above, We Will Use Polar Coordinates.
Web polar equations of conic sections: Aj speller · · sep 28 2014. First, we should expand the expression: A locus of points is a set of points, each location of which is satisfied by some condition.
Web Then The Polar Equation For A Conic Takes One Of The Following Two Forms:
Graph the polar equations of conics. For a conic with a focus at the origin, if the directrix is x= ±p, x = ± p, where p p is a positive real number, and the eccentricity is a positive real number e, e, the conic has a polar equation. Web the polar form of the equation of a conic is often used in dynamics; Represent \(q\left( x,y \right)\) in polar coordinates so \(\left( x,y \right) = \left( r\cos (\theta ), r\sin (\theta ) \right)\).
For Each Of The Following Equations, Identify The Conic With Focus At The Origin, The Directrix, And The Eccentricity.
Web given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity. Hyperbola → a ⋅ c < 0. If the directrix is a distance d d away, then the polar form of a conic section with eccentricity e e is. Identifying a conic given the polar form.